Evolusjonær informatikk:

Marks, Dembski og Ewert demonstrerer: grensene til darwinismen

(kursiv og understreking ved oversetter)
Brian Miller; 2. mai, 2017; Oversatt herfra.

Bilde 1: Mandelbrot sett, detalj, av Binette228 (eget arbeid) [ CC BY-SA 3.0 ], via Wikimedia Commons.

I utviklingsdebatten er et sentralt tema evnen naturlig utvalg har til å produsere komplekse innovasjoner. I en tidligere artikkel forklarte jeg (Br. Miller) på grunnlag av ingeniørteorier om innovasjon, hvorfor småskala endringene som driver mikroevolusjonen ikke burde kunne akkumuleres for å generere de store endringene som kreves for makroevolusjon. Denne observasjonen tilsvarer perfekt forskning i utviklingsbiologi og mønsteret til fossilregistreringen. Begrensningene til den darwinistiske evolusjonen er imidlertid blitt demonstrert enda sterkere fra feltene for evolusjonær beregning og matematikk. Disse teoretiske utfordringene er detaljert i en ny bok ut denne uken, Introduksjon til Evolusjonær Informatikk -her.

Forfattere Robert Marks, William Dembski og Winston Ewert bringer tiår med erfaring i søkealgoritmer og informasjonsteori for å analysere kapasiteten til biologisk evolusjon for å generere ulike former for liv. Deres konklusjon er at ingen evolusjonær prosess er i stand til å gi forskjellige utfall (f.eks. nye kroppsplaner), i stedet er de begrenset til et svært begrenset utvalg av resultater (f.eks finker med forskjellige nakkestørrelser). For å produsere noe av betydelig kompleksitet, kreves at kunnskap om resultatet programmeres inn i søkerutinen. Derfor er ethvert krav på ubegrenset kapasitet til ikke-styrt evolusjon for å forandre livet, nødvendigvis uakseptabelt.

Forfatterne begynner sin diskusjon ved å gi litt nødvendig bakgrunn. De presenterer en oversikt over hvordan informasjon er definert, og definerer standardmålinger av KCS (Kolmogorov-Chaitin-Solomonov) kompleksitet og Shannon-informasjon -her . Førstnevnte gir det minste antall biter som kreves for å gjenta et mønster - maksimal komprimerbarhet. Sistnevnte angår loggen av sannsynligheten for at et mønster kommer frem som et resultat. For eksempel er sannsynligheten for å snurre fem mynter og ha dem alle land på 'kron' 1/32.

Informasjonsinnholdet i KKKKK er da den negative log(2) (1/32), som er 5 (bits). Mer enkelt, et bestemt utfall av 5 myntkast tilsvarer 5 biter av informasjon.
De beskriver hvordan søk i ingeniørfag for noen designutfall involverer de tre komponentene i domenekompetanse, designkriterier og iterativt søk. Prosessen innebærer å lage en prototype og deretter sjekke for å se om den oppfyller kriteriene, som fungerer som et teleologisk mål. Hvis det opprinnelige designet ikke gjøres, blir prototypen raffinert og testen gjentas. Jo større domenekompetanse, desto mer effektive tilpasninger blir gjort, så må færre muligheter testes. Suksessen kan da oppnås raskere.

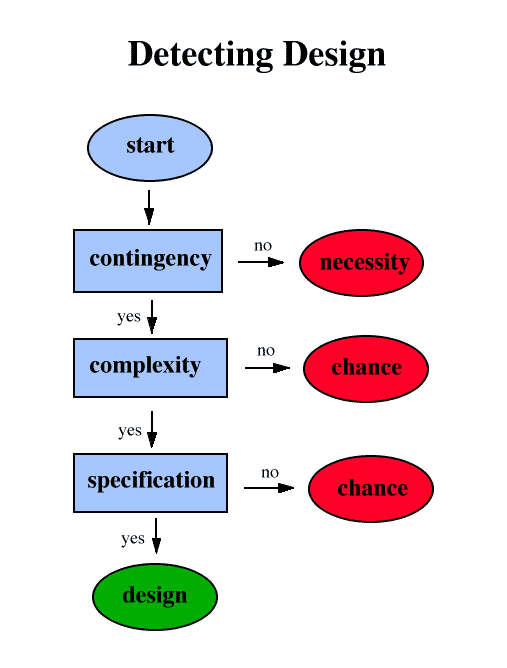
Bilde 2. Et Dembski-bidrag

De demonstrerer denne prosessen med et hjemlig eksempel: steking av pannekaker. Det første tilfellet innebærer å justere tiden pannekaker ble tilberedt på forsiden og på baksiden. En første pannekake ble tilberedt i to tilfeldige tider, og det ble deretter smakt. Basert på smaken ble temperaturene deretter justert for den andre iterasjonen. Denne prosessen ble gjentatt til en pannekakes smak møtte en kvalitetsterskel. For fremtidige tilfeller ble det tilsatt ytterligere variabler, for eksempel mengden melk som brukes i røren, temperaturinnstillingen og den tilsatte mengden salt. Hvis hver variabel ble tildelt en verdi mellom 1 og 10, slik som de ti innstillingene på komfyren, økte antall mulige forsøk med en faktor 10 for hver ny variabel. Antall muligheter vokser veldig raskt.

For atskillige variabler, hvis forsøkspersonen ikke hadde kjennskap til matlagingen, ville tiden som var nødvendig for å finne et passende utfall være 'avskrekkende lenge'. Men med større kunnskap kan det gjøres bedre valg for å redusere antall nødvendige søk. For eksempel vil en erfaren kokk (det vil si en kokk med større domeneerfaring) vite at tiden på begge sider skal være omtrent det samme, og pannekaker som er for vannrike krever ekstra mel.

Dette eksemplet følger den grunnleggende tilnærmingen til felles evolusjonære design søk. Hovedforskjellen er at flere forsøk ofte kan simuleres på en datamaskin samtidig. Deretter kan hvert individ bli uavhengig testet og endret. Komponentene i hver syklus inkluderer en fitness-funksjon (aka oracle) for å definere ett eksemplars status (for eksempel smak av pannekaken), en metode for å bestemme hvilke enkelt-ingredienser som er fjernet og som forblir eller dupliseres, og hvordan enkelt-ingredienser endres for neste iterasjon (f.eks. mer melk). Forfatterne gir flere eksempler på hvordan slike evolusjonære algoritmer kunne brukes til forskjellige problemer. En av de mest interessante eksemplene de gir, er hvordan NASA brukte en evolusjonær algoritme for å bøye en lengde ledning til en effektiv X-band-antenne -her.

På denne måten demonstrerer forfatterne begrensningene til evolusjonære algoritmer. Den generelle utfordringen er at alle evolusjonære algoritmer er begrenset til konvergering på et svært smalt utvalg av resultater, en grense kjent som Basener's Ceiling. For eksempel konvergerer et program designet for å produsere en antenne til løsningen av en optimal antenne og forblir deretter fast. Det kan aldri generere noe helt annet resultat, for eksempel en musefelle. Alternativt kan en algoritme designet for å generere en strategi for å spille sjakk aldri generere en strategi for å spille backgammon. For å endre utfallet, må programmet på en bevisst måte justeres for å oppnå et eget forutbestemt mål. I sammenheng med evolusjonen kan ingen uklar prosess konvergere på en organisme, som en fisk, og deretter konvergere senere på et amfibium.

Dette prinsippet har blitt demonstrert både i simuleringer og i eksperimenter. Programmet Tierra -her, ble opprettet i håp om å simulere storskala biologisk evolusjon. Resultatene var skuffende. Flere simulerte organismer oppstod, men deres variabilitet rammet snart Basener's Ceiling. Ingen sann nyhet ble generert, men bare begrensede om-arrangeringer av den innledende informasjonen. Vi har sett et lignende resultat i eksperimenter på bakterier av Michigan State biolog Richard Lenski -her. Han spores utviklingen av 58.000 generasjoner av E. coli . Han så ingen sann innovasjon, men primært ødeleggelse av ikke-essensielle gener for å spare energi , og omarrangering av genetisk informasjon for å få tilgang til eksisterende kapasiteter, som for eksempel stoffets metabolisme -her , under forskjellige miljøbelastninger. Endringer var alltid smale i omfang og begrenset i størrelse.

Bilde 3. Case i Tierra-programmet

Forfatterne presenterer en enda mer begrensende begrensning, basert på 'No Free Lunch Theoremene', som er kjent som Conservation of Information (COI). Enkelt sagt, ingen søkestrategi kan i gjennomsnitt finne et mål raskere enn et tilfeldig søk, med mindre noe informasjon om det målet er innlemmet i søkeprosessen. Som en illustrasjon, forestill deg noen som ber deg om å gjette navnet på en berømt person, men uten å gi deg noen informasjon om den personen. Du kan bruke mange forskjellige gjetningsstrategier, for eksempel å oppgi kjente personer du kjenner i alfabetisk rekkefølge, eller etter høyde, eller etter fødselsdato. Ingen strategi kunne bestemmes på forhånd for å være bedre enn et tilfeldig søk.
Men hvis du fikk lov til å stille en rekke spørsmål, vil svarene gi deg informasjon som kan bidra til å begrense eller veilede søket. For eksempel, hvis du ble fortalt at den berømte personen var nålevende, ville det dramatisk redusere søkeområdet. Hvis du da lærte personen var en skuespiller, ville du ha enda mer veiledning om hvordan å gjette. Eller kanskje du vet at personen er en fan av science fiction, i så fall kan du fokusere gjetting på folk som er tilknyttet sci-fi-sjangeren.

Vi kan forstå ordningen mer kvantitativt. Størrelsen på ditt opprinnelige søkerom kan defineres i forhold til Shannon-informasjonen. Hvis du visste at en av 32 kjente personer var målet, ville søkeområdet svare til log2(32), som er 5 (bits). Denne verdien er kjent som den endogene informasjonen i søket. Informasjonen som er gitt på forhånd for å hjelpe søket, kalles den aktive informasjonen. Hvis du fikk informasjon som eliminert alle untatt 1/4 av de mulige valgene, ville du ha log2(4), som er 2 (bits) av aktiv informasjon. Informasjonen assosiert med å finne målet i det reduserte søkeområdet er da log2(32/4), som er 3 (bits). Den søk-relaterte informasjonen er bevart: 5 bits (endogen) = 2 bits (aktiv) + 3 bits (gjenværende søkerom).

Bilde 4. Begrenset hva som kan skje i universets levetid

COI-teoremet gjelder for alle evolusjonære søk. NASA-antenne-programmet virker bare fordi det bruker en søkemetode som inneholder informasjon om effektive antenner. Andre programmer som er utformet for å simulere evolusjon, som Avida, er også utstyrt med den nødvendige aktive informasjonen for å generere de ønskede resultatene. I motsetning er den biologiske utviklingen rettet mot blindt naturlig utvalg, som ikke har noen aktiv informasjon som kan hjelpe til med å søke etter nye mål. Prosessen er ikke hjulpet av endringer i miljøet, noe som endrer egnethetslandskapet, siden slike endringer ikke inneholder aktiv informasjon relatert til et radikalt annet utfall.

Til slutt er den endogene informasjonen som er knyttet til å finne en ny kroppsplan eller en annen signifikant modifikasjon, langt større enn det som er forbundet med søkerommet som biologiske avkom muligens kan utforske i hele universets alder. Derfor, som disse forfatterne tydelig viser, i tråd med mye tidligere forskning innen intelligent design, krevde alle radikale innovasjoner i naturen, informasjon fra en utenforliggende intelligent kilde.

Tager:
Shannon informasjon; W.Dembski; R. Lenski;